Finding the Domain of a Function
OK, so suppose we don't have the graph of a function to look at like in the last section...
Can we still find the domain and range?
So, we'll just be doing domains on these -- which is really where the action is anyway.
Asking for the
domain of a function
is the same as asking
"What are all the possible
x
guys
that I can stick into this thing?"
Sometimes, what you'll really be looking for is
"Is there anything I CAN'T stick in?"
Check it out:
Do you see any
x
guys
that would cause a problem here?
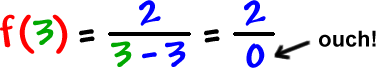
So,
x
=
3
is a bad guy! Everyone else is OK, though.
The domain is all real numbers except
3
.
What would the interval notation be?
When in doubt, graph it on a number line:
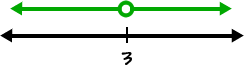Do the interval notation in two pieces:
YOUR TURN:
Sometimes, you can't find the domain with a quick look.
Check it out:
Hmm... It's not so obvious!
BUT, we are still looking for the same thing:
How do we find it? Easy!
Set the denominator =
0
and solve!
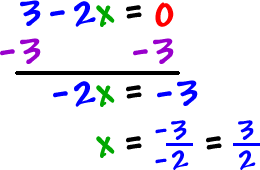
TRY IT:
How about this one?
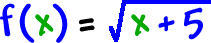Square roots -- what do we know about square roots?
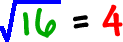... So,
16
is OK to put in.
... So,
0
is OK.
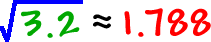... Yuck! But,
3.2
is OK.
... Nope! Can't do it!
*We only want real numbers!
No negatives are OK!
The
inside
of aradical
cannot be negative if we wantreal answers
only (no
i
guys). So, the
inside
of aradical
has to be0 or a positive number
.
Now, let's find the domain of
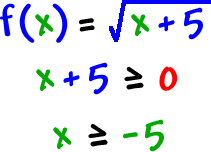
TRY IT:
Here's a messier one:
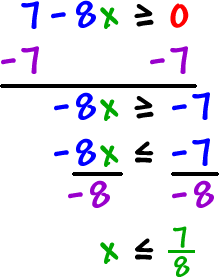
Can we still find the domain and range?
Domains : |
Yes (as long as the algebra doesn't get too hairy... and it won't for us.) |
Ranges : |
Not really (you usually need the picture -- unless it's something really basic.) |
So, we'll just be doing domains on these -- which is really where the action is anyway.
Asking for the
domain of a function
is the same as asking
"What are all the possible
x
guys
that I can stick into this thing?"
Sometimes, what you'll really be looking for is
"Is there anything I CAN'T stick in?"
Check it out:
| Let's find the domain of |  |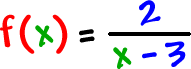
x
guys
that would cause a problem here?
| What about |  |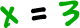
? |
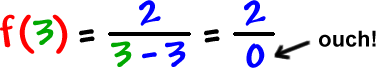
So,
x
=
3
is a bad guy! Everyone else is OK, though.
The domain is all real numbers except
3
.
What would the interval notation be?
When in doubt, graph it on a number line:
| domain |  |
YOUR TURN:
| Find the domain of |  |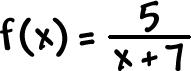
Sometimes, you can't find the domain with a quick look.
Check it out:
| Let's find the domain of |
 |
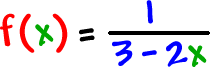BUT, we are still looking for the same thing:
 |
The bad x that makes the denominator 0 ! |
Set the denominator =
0
and solve!
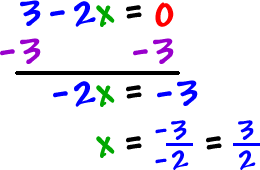
| The domain is |
 |
TRY IT:
| Find the domain of |  |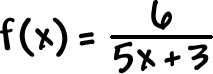
*show work!! |
How about this one?
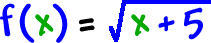
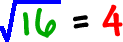... So,16
is OK to put in.
... So,0
is OK.
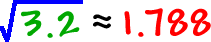... Yuck! But,3.2
is OK.
... Nope! Can't do it!*We only want real numbers!
No negatives are OK!
inside
of aradical
cannot be negative if we wantreal answers
only (no
i
guys). So, the
inside
of aradical
has to be0 or a positive number
.
| Set |  |
and solve it! |
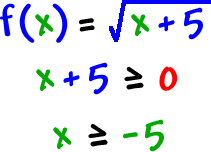
| So, the domain of |  |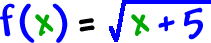
is |  |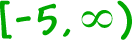
. |
TRY IT:
| Find the domain of |  |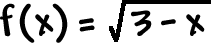
. *Show work!! |
Here's a messier one:
| Let's find the domain of |  |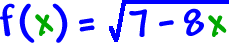
Set |
 |
and solve! |
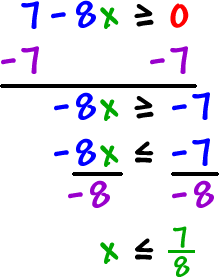
| The domain is | ![( -infinity , 7 / 8 ]](https://www.coolmath.com/sites/default/files/images/06-functions-25.gif) |
. |
from Fruitty Blog https://ift.tt/2ZQbMTF
via IFTTT
No comments:
Post a Comment